Argos User Manual
PrevChapter 13. Housekeeping FunctionsNext

Add Lowess Curve

This operation is only available in the right-click menus of scatterplots and sum-difference plots. What it does depends on if there is a ✓ mark to its left in a right-click menu.

When there is no ✓ mark:

It adds a lowess curve to the point cloud to help you better perceive the relationship between the 2 variables plotted on the horizontal and the vertical axes.

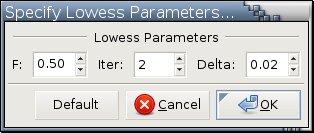
If the Shift key is held down when this operation is invoked from the right-click menu [1], a dialog like

---> images/hkf-add-lowess-curve-arg-menu.png <---

will pop up for you to specify the following 3 parameters: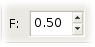

  • F specifies the amount of smoothing and is the fraction of points used to compute each fitted value. As F increases the curve becomes smoother. Choosing F in the range 0.2 to 0.8 usually results in a good fit. The default is 0.5.

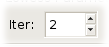  • Iter is the number of iterations in the robust fit. If Iter is 0, the nonrobust fit is returned. Setting Iter equal to 2, the default, should serve most purposes.

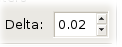  • Delta is a number between 0.0 and 1.0 and may be used to save computations. If the number of points of unique X coordinates is less than 100, set Delta equal to 0.0. If there are more than 100 points of unique X coordinates, setting Delta to 0.02, the default, often works well. Read this footnote [2] for more information on how to choose Delta.

If the Shift key is not held down when this operation is invoked, a lowess curve will be fitted and drawn using either the lowess parameters specified last time when Shift-<Add Lowess Curve> is invoked or the default values (0.5 for F, 2 for Iter, and 0.02 for Delta) if Shift-<Add Lowess Curve> has never been invoked.

When there is a ✓ mark:

The plot on which this operation is invoked is already displaying a lowess curve. This operation will remove the lowess curve being displayed.

If this operation is invoked from a panel plot [3] of a trellis display, the end effect is equivalent to invoking Add Lowess Curves on the associated trellis display.

Notes

[1]

Shift-<Add Lowess Curve> for short.

[2]

Suppose a lowess curve is to be fitted to a point cloud: (Xi, Yi), i = 1, 2, ..., N. Sort these N pairs of numbers according to values of Xi's, from the smallest to the largest. Reassign subscripts to these N pairs of numbers so that X1 becomes the smallest and XN becomes the largest. Use X to denote the vector of X1, X2, ..., XN. Delta is a number between 0.0 and 1.0, inclusive. Define DELTA to be Delta*(XN-X1). On the initial fit and on each of the Iter iterations locally weighted regression fitted values are computed at points in X which are spaced, roughly, DELTA apart; then the fitted values at the remaining points are computed using linear interpolation. The first locally weighted regression (l.w.r.) computation is carried out at X1 and the last is carried out at XN. Suppose the l.w.r. computation is carried out at Xi. If Xi+1 is greater than or equal to Xi+DELTA, the next l.w.r. computation is carried out at Xi+1. If Xi+1 is less than Xi+DELTA, the next l.w.r. computation is carried out at the largest Xj which is greater than or equal to Xi but is not greater than Xi+DELTA. Then the fitted values for Xk between Xi and Xj, if there are any, are computed by linear interpolation of the fitted values at Xi and Xj. If N is less than 100 then Delta can be set to 0.0 since the computation time will not be too great. For larger N it is typically not necessary to carry out the l.w.r. computation for all points, so that much computation time can be saved by taking Delta to be greater than 0.0. If Delta = 1/k then, if the values in X were uniformly scattered over the range, the full l.w.r. computation would be carried out at approximately k points. Taking k to be 50 often works well.

[3]

Unlimited panel plots do not exhibit this behaviour.

PrevHomeNext
Add Linear Regression LinesUpAdd Lowess Curves