Linear Regression

• Arguments: Numerical variables

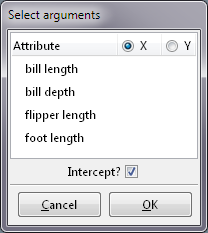
• Argument menu:

  • Example:

    

    ---> images/analytical-lsfit-arg-menu.png <---

  • This menu allows multiple variables to be selected as X variables (independent variables or carriers) but only allows one variable to be selected as Y variable (dependent or response variable).

  • When selecting X variables, use Left , Ctrl-Left , and Shift-Left . See here for details.

• Available modes: , , , , and .

• Housekeeping functions:

  Activate Circle Antialiasing Globally	Add Lowess Curve	Categorize by Colors...
  Comment...	Copy	Save as PNG Image...
  Set Axis Labels...	Set Background...	Set Screen Size Same as...
  Set as Default Plot Size	Set Drawing Ranges Same as...	Shrink to Min Drawing Ranges
  Summarize Data

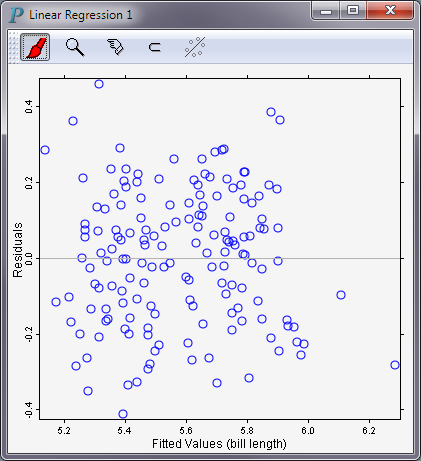
• Example: Figure 12-1

  Figure 12-1. Linear Regression

  

  ---> images/analytical-lsfit-example.png <---

  The output of a linear regression run is presented as a residual plot, which is a scatterplot of fitted-values versus residuals.

Let

represent a set of n measurements of p independent variables and 1 dependent variable. We define the general linear regression model simply in terms of the p X variables: where Linear Regression estimates β₀, β₁, ..., β_p by least squares. When Intercept? is not checked, β₀ is set to zero before the rest parameters are estimated by least squares.

Let b₀, b₁, ..., b_p be the least squares estimates of β₀, β₁, ..., β_p. The fitted values are

The residuals are